Do you even entangle qubits?

In the previous post, we described what qubit is. As a quick reminder, a qubit is a quantum analog of a bit, a simple two-state quantum system with all of the quantum peculiarities. Just as a classical bit can be in 0 and 1 states, a qubit can be in $\lvert 0 \rangle$ and $\lvert 1 \rangle$ states. One of the qubit’s traits is the ability to be in a superposition, $\lvert \phi \rangle = \alpha \lvert 0 \rangle + \beta \lvert 1 \rangle$. Superposition means that if we measure that qubit state multiple times we will get $\lvert 1 \rangle$ with ${\lvert \alpha \rvert}^2$ probability and ${\lvert \beta \rvert}^2$ probability.

Product states

It seems that qubits are social beings, hence let’s consider a two-qubit state $\lvert ba \rangle$. During measurement this system can be in four states - $\lvert 00 \rangle$, $\lvert 01 \rangle$, $\lvert 10 \rangle$, $\lvert 11 \rangle$. Of course, each of those base states has an associated amplitude which is a product of its components’ amplitudes.

\[\lvert a \rangle = \alpha_a \lvert 0 \rangle + \beta_a \lvert 1 \rangle \\ \lvert b \rangle = \alpha_b \lvert 0 \rangle + \beta_b \lvert 1 \rangle \\ \lvert ba \rangle = \alpha_b \cdot \alpha_a \lvert 00 \rangle + \alpha_b \cdot \beta_a \lvert 01 \rangle + \beta_b \cdot \alpha_a \lvert 10 \rangle + \beta_b \cdot \beta_a \lvert 11 \rangle\]

The same limitation is placed on amplitudes, meaning that the sum of their modulus squares needs to be equal to $1$

\[{\lvert \alpha_b \cdot \alpha_a \rvert}^2 + {\lvert \alpha_b \cdot \beta_b \rvert}^2 + {\lvert \beta_b \cdot \alpha_a \rvert}^2 + {\lvert \beta_b \cdot \beta_a \rvert}^2 = 1\]

To close on this very brief introductory description, let us go through an example two-qubit state $\lvert -1 \rangle$ (that is read “ket minus 1”)

\[\lvert - \rangle = \frac{1}{\sqrt{2}} \lvert 0 \rangle - \frac{1}{\sqrt{2}} \lvert 1 \rangle \\ \lvert 1 \rangle = 0 \lvert 0 \rangle + 1\lvert 1 \rangle \\ \lvert - 1 \rangle = (\frac{1}{\sqrt{2}} \cdot 0) \lvert 00 \rangle + (\frac{1}{\sqrt{2}} \cdot 1) \lvert 01 \rangle - (\frac{1}{\sqrt{2}} \cdot 0) \lvert 10 \rangle - (\frac{1}{\sqrt{2}} \cdot 1) \lvert 11 \rangle \\= \frac{1}{\sqrt{2}}(\lvert 01 \rangle - \lvert 11 \rangle)\]

With amplitudes described above, we have a 0.5 probability of observing $\lvert 01 \rangle$ and a 0.5 probability of observing $\lvert 11 \rangle$.

Canceling out amplitudes

As you might recall the amplitudes are complex numbers. That means that the $-\frac{1}{\sqrt{2}}\lvert 11 \rangle$ is completely valid as for example $-\frac{i}{\sqrt{4}}\lvert 11 \rangle$ would be (although the rest of amplitudes would have to be different). That means that with an interesting enough chain of quantum logic gates, some amplitudes will cancel each other out! (Recall $i^2 + 1^2 = 0$).

Entangled states

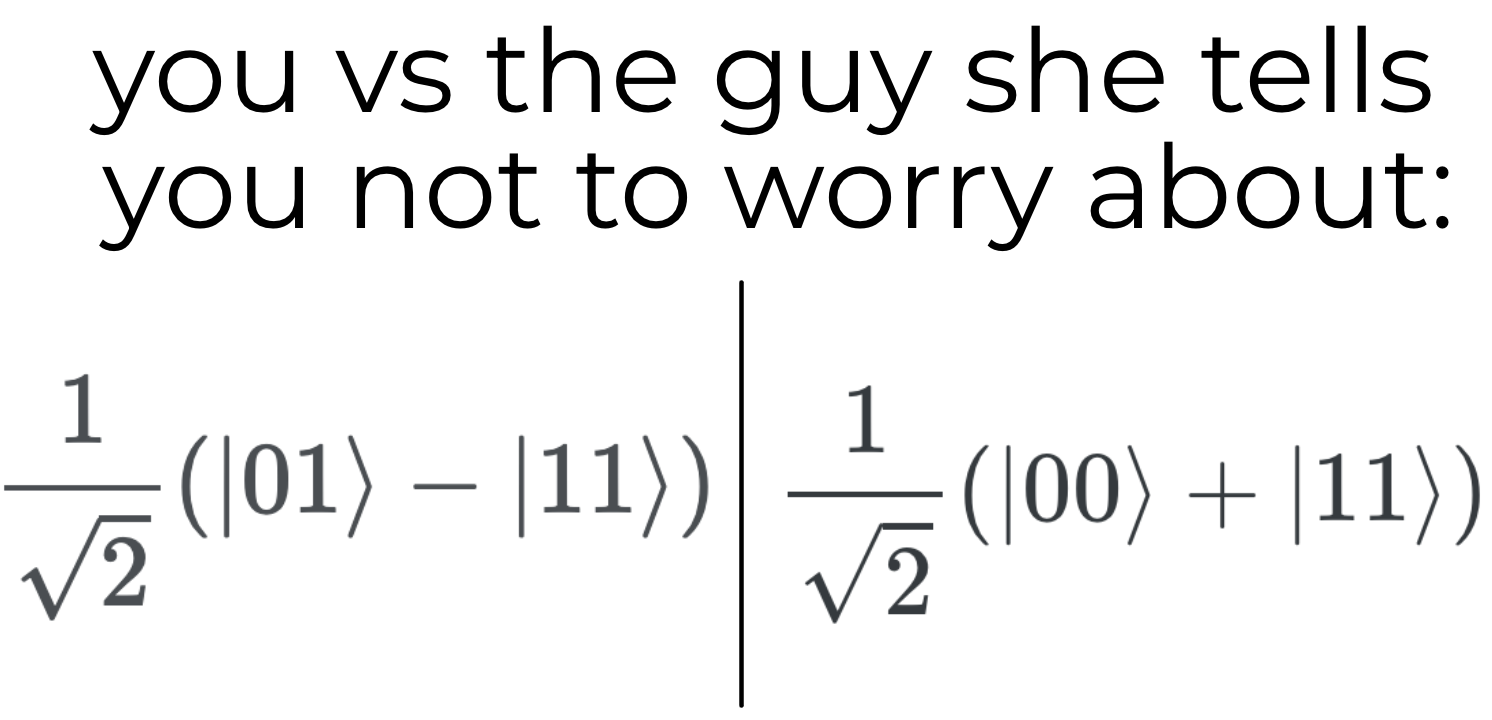
Okay, we described multiple qubit states. You might scratch your head “Well, so what?”.

It turns out that we can have states that are not a product of individual qubit states! Consider the following state (read “ket phi plus”)

\[\lvert \Phi^+ \rangle = \frac{1}{\sqrt{2}}(\lvert 00 \rangle + \lvert 11 \rangle)\]

We can play a little with this state

\[\lvert \Phi^+ \rangle = \alpha_b \cdot \alpha_a \lvert 00 \rangle + \alpha_b \cdot \beta_a \lvert 01 \rangle + \beta_b \cdot \alpha_a \lvert 10 \rangle + \beta_b \cdot \beta_a \lvert 11 \rangle \\ \frac{1}{\sqrt{2}}\lvert 00 \rangle - \frac{1}{\sqrt{2}}\lvert 11 \rangle = \alpha_b \cdot \alpha_a \lvert 00 \rangle + \alpha_b \cdot \beta_a \lvert 01 \rangle + \beta_b \cdot \alpha_a \lvert 10 \rangle + \beta_b \cdot \beta_a \lvert 11 \rangle \\ \alpha_b \cdot \alpha_a = \frac{1}{\sqrt{2}} \text{ (eq. 1)} \\ \alpha_b \cdot \beta_a = 0 \text{ (eq. 2)}\\ \beta_b \cdot \alpha_a = 0 \text{ (eq. 3)}\\ \beta_b \cdot \beta_a = -\frac{1}{\sqrt{2}} \text{ (eq. 4)}\\\]

Okay, so let us tackle this problem with basic equation-solving skills! If we look at equations 1 and 2, we can deduce that $\alpha_b \neq 0$, otherwise we could not satisfy equation 1. That implies that $\beta_a$ is $0$. Whew, that was close! But if we look at equation 4 now, we end in a ditch, because it cannot be satisfied with $beta_a = 0$. This short reasoning shows that we cannot represent the $\lvert \Phi^- \rangle$ state by simply combining states of two single qubits.

So how could we achieve that?

With the help of quantum logic gates, obviously! We know that we can achieve $\lvert -1 \rangle$ state. We are missing a gate that would have a $4 \times 4$ matrix that would map (for example ) $\lvert -1 \rangle$ to $\lvert \Phi^- \rangle$. That means solving $\lvert \Phi^- \rangle = M \cdot \lvert -1 \rangle$. Moreover, to meet the requirements of a quantum logic gate, we need to ensure that $M$ is unitary. With some tinkering, we can get to

\[M = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \\ \end{bmatrix}\]

To sum up, we started with two qubits in a product state pushed those qubits through a gate, and ended up in an entangled state that cannot be split into two qubits.

Why do we even need entangled states?

Okay, we described entangled qubit states. You might scratch your head “Well, so what?”.

Quantum algorithms you might read about leverage entanglement to propose solutions that are computationally faster than the fastest known “classical” algorithms. This is why we need to grasp the idea of the entangled state.

I do not know whether an entangled state is strictly necessary for a quantum algorithm to have a “quantum advantage”, but there are voices saying that it is necessary. On the other hand there are papers showing that there is a possible quantum advantage even without the entangled state. My opinion - as a layman - is anything realizable and practically useful will need entanglement along the way.